在用 Keras 疊一個手寫數字辨識神經網路時，有幾個名詞要先知道一下。而今天要介紹的是 activation function，中文翻成激勵函數、激活函數或作用函數等。

下面分成「什麼是激勵函數(activaiton function)？」、「為什麼要用激勵函數？」和「激勵函數有哪些及其優缺」三項介紹。

一、什麼是激勵函數(activaiton function)？

我們前幾天有提到，神經網路是由一顆顆「人造神經元」所組成，而細看神經元，會發現它是由輸入(input)、權重(weight)、誤差(bias)及激勵函數(activation function)所組成。

這幾個詞是什麼意思呢？我們知道，機器學習的過程就是在找一個函式(function)，而通常在找輸入跟目標之間的 function 時，如果要自己假設方程式，簡單假設線性 y=ax+b 是一個蠻直覺的選項。

neuron 的假設也是一樣，我們假設每一個 neuron 就是 y=∑wx+b，我們預期的輸出是由多個 input 去乘上每個 input 的重要性(weight)，加上一個常數(bias)就可以得到我們想要的輸出。然而線性有它的限制在，所以我們加上一個激勵函數(activation function) 去引入非線性，讓它更像一般情形。

ps. 這邊的講法偏向以目的性去解釋激勵函數是什麼，及它在 Neuron 數學式的作用，實際上激勵函數的出現應該要從邏輯迴歸和機率方面推出。

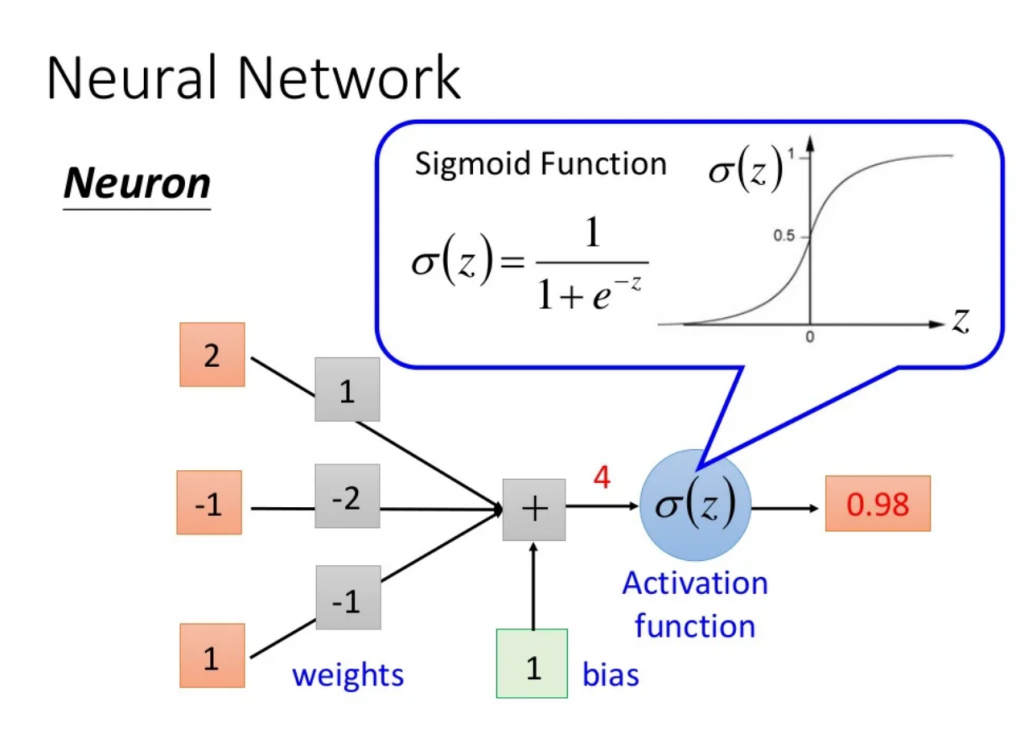
圖片來源：李宏毅老師的機器學習課程

二、為什麼要用激勵函數？

這邊引用 深度學習：使用激勵函數的目的、如何選擇激勵函數 Deep Learning : the role of the activation function 所說的使用激勵函數的目的：

在類神經網路中如果不使用激勵函數，那麼在類神經網路中皆是以上層輸入的線性組合作為這一層的輸出（也就是矩陣相乘），輸出和輸入依然脫離不了線性關係，做深度類神經網路便失去意義。

三、激勵函數有哪些類型？

常見的激勵函數有 sigmoid, ReLU 跟 softmax 等，若想多了解一點可以看如 Keras 套件激勵函數的官方預設文檔，這邊先簡單介紹常見的三種：

1. sigmoid (圖片來源)

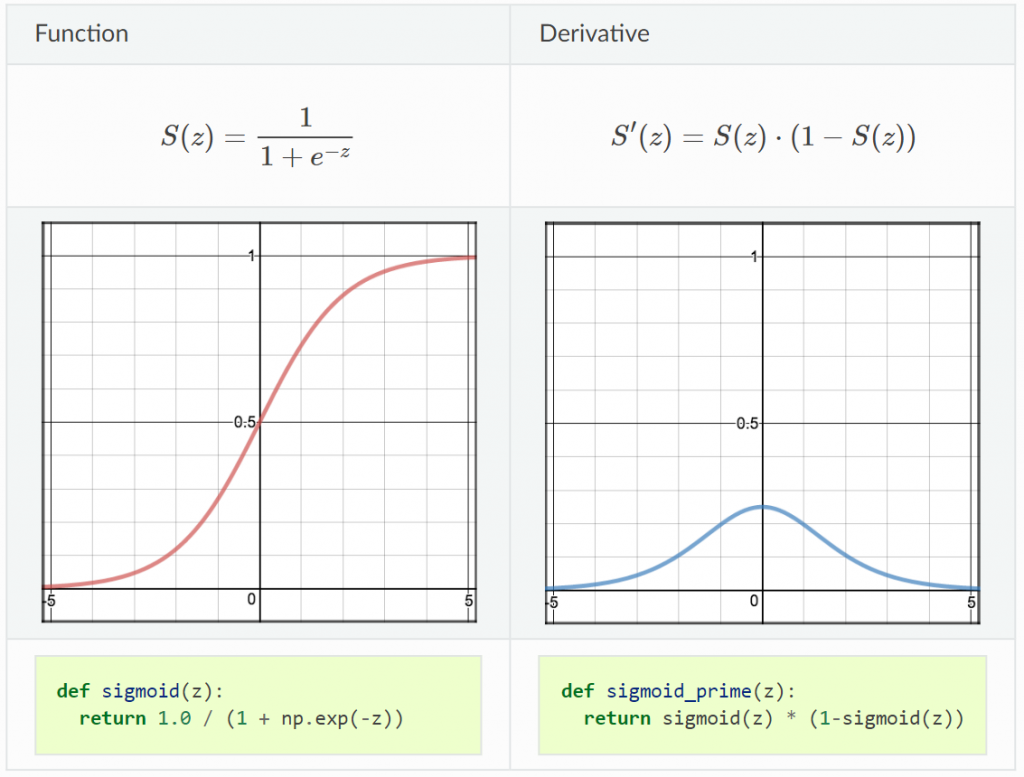
output 範圍：0~1 (y軸)

優：適合用在輸出層做二分類 (將小於 0.5 的值歸在 0、大於 0.5 的值歸在 1)

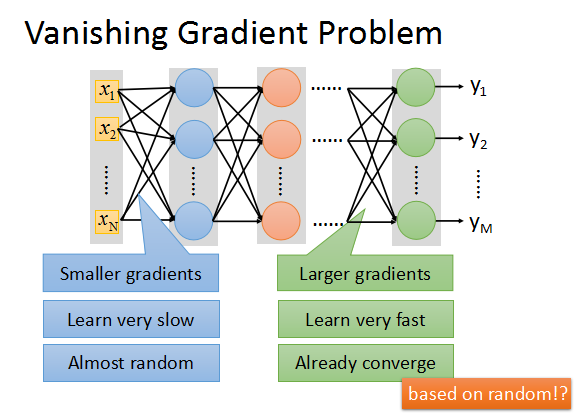
缺：會有梯度消失問題 (前面層的參數還是 random 的狀態，後面層已經收斂到區域最小值了)

這邊推薦看 ML Lecture 9-1: Tips for Training DNN (12:30 ~ 35:30)，李宏毅老師解釋了什麼是梯度消失問題(Vanishing Gradient Problem)，以及使用 ReLU 來改善這個問題的由來、ReLU的優缺等。

2. ReLU(Rectified Linear Unit)

output 範圍：input 小於 0 時 = 0，input 大於 0 時 = input

優：1. 運算快，不像 sigmoid 有指數運算
2. 像生物學神經傳導上的全有全無律
3. 是無限多個 sigmoid 疊加起的結果
4. 可以解決梯度消失問題

缺：有 Dying ReLU problem，所以有變形 Leaky ReLU 或延伸 maxout 等方法

實務上常使用此類方法。不過這邊可能會有人問一個問題是，ReLU 看起來是線性的，這樣神經網路不就又變成線性的嗎？ -> ReLU 並不是線性，它是分段線性或說局部線性，但整體不是線性的，證明如下截圖來源：

3. softmax

softmax 用程式表示其概念最快 XD

import numpy as np

inputs = np.array([1, 3, 5, 7, 9])

def softmax(inputs):
  return np.exp(inputs) / sum(np.exp(inputs))

outputs = softmax(inputs)
print('outputs=', outputs)
print('')

print('{} -> {}'.format('inputs', 'outputs'))
for i in range(len(outputs)):
  print('{} -> {}'.format(inputs[i], outputs[i]))

output：適合用在輸出層做多分類，softmax 的輸出總和=1

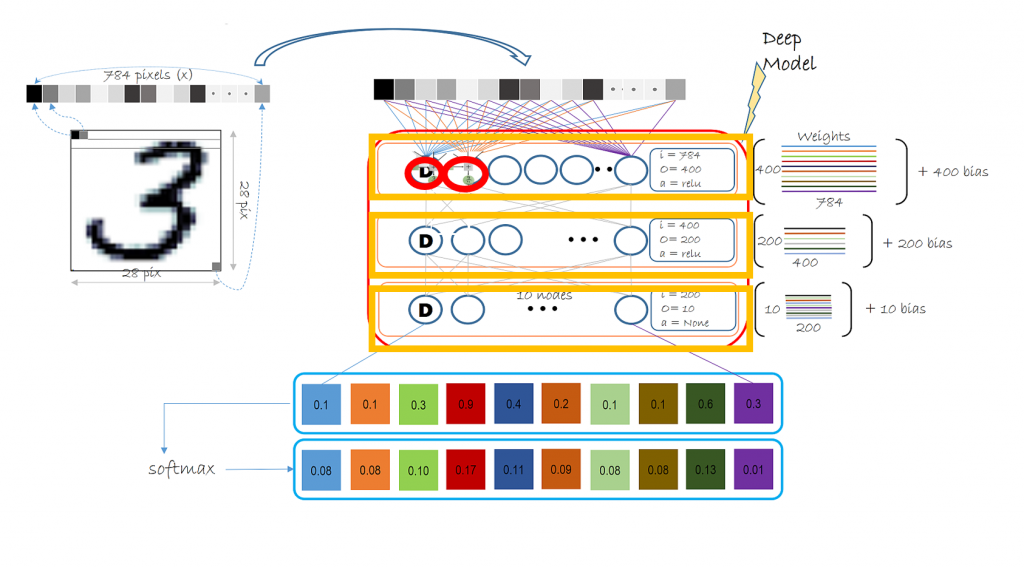
這邊補充一下 day5 的圖，我們在用 Keras 套件像堆積木的方式(如下圖橘框)新增一層一層神經網路功能，最後輸出層使用 softmax，它會輸出一個輸出總和為1的list，輸出 input 這張圖在每一類型 output 的可能機率，最後判斷成機率最大的那一類。

4. 小結

今天簡單講了 什麼是激勵函數(activaiton function)、為什麼要用激勵函數和sigmoid, ReLU 跟 softmax三個激勵函數及其優缺，希望大家都有看懂～

ps.每天文章字數越寫越多了